Exponentialfunktionen

• Aufgaben

Mit dem Taschenrechner berechnen wir folgende Werte:

• \(e^{1}=2.718281828\)

• \(e-\left(1+\frac{1}{100}\right)^{100}\approx 0.013468\)

• \(e-\left(1+\frac{1}{1000}\right)^{1000}\approx 0.0013579\)

• \(e-(1+\frac{1}{1000000})^{1000000}\approx 0\)

Damit können wir den Wert von \(e\) als Grenzwert angeben.

\(\underset{n\rightarrow+\infty}{\lim}(1+\frac{1}{n})^{n}=e\)

---

Auch die Werte \(e^{2}\), \(e^{5}\) oder \(e^{x}\) geben wir als Grenzwerte an.

• \(\underset{n\rightarrow+\infty}{\lim}(1+\frac{2}{n})^{n}=e^{2}\)

• \(\underset{n\rightarrow+\infty}{\lim}(1+\frac{5}{n})^{n}=e^{5}\)

• \(\underset{n\rightarrow+\infty}{\lim}(1+\frac{x}{n})^{n}=e^{x}\)

---

Allgemein gilt:

Die Funktion

\(f:x\mapsto e^{x}=\underset{n\rightarrow+\infty}{\lim}(1+\frac{x}{n})^{n}\) mit \(x\in\mathbb{R}\)

heißt natürliche Exponentialfunktion.

Die Zahl \(e=2.71828182\ldots\) ist die eulersche Zahl. Für alle \(x\in\mathbb{R}\) ist \(f(x)=e^{x}>0\). Die natürliche Exponentialfunktion hat den Wertebereich \(W_{f}=\mathbb{R}^{+}\) und somit keine Nullstellen.

---

Für die natürliche Exponentialfunktion gelten folgende wichtige Rechenregeln:

• \(e^{a}\cdot e^{b}=e^{a+b}\) und \(\frac{e^{a}}{e^{b}}=e^{a-b}\) mit \(a,b\in \mathbb{R}\)

• \(\left( e^{a}\right)^{b}=e^{a\cdot b}\)

• Beachte: \(e^{a^{b}}\neq \left( e^{a}\right)^{b}=e^{a\cdot b}\), also \(e^{a^{b}}\neq e^{a\cdot b}\)

• \(e^{-a}=\frac{1}{e^{a}}\) oder \(e^{a}=\frac{1}{e^{-a}}\)

• \(e^{\frac{a}{w}}=\sqrt[w]{e^{a}}\) mit \(w\in\mathbb{R}\setminus\left\{ 0\right\}\)

• \(e^{-\frac{a}{w}}=\frac{1}{\sqrt[w]{e^{a}}}\) oder \(e^{\frac{a}{w}}=\frac{1}{\sqrt[w]{e^{-a}}}\)

---

Exponentialterme sind streng von Potenzterme zu unterscheiden. Potenzterme haben eine feste Hochzahl und eine variable Basis, z. B. \(x^{3}\). Exponentialterme haben eine feste Basis und eine variable Hochzahl, z. B. \(3^{x}\).

---

Die Umkehrung der Exponentialrechnung ist die Logarithmusrechnung.

\(e^{a}=p\Leftrightarrow a=\log_{e}p\) (Logarithmus zur Basis \(e\) von \(p\in\mathbb{R}^{+}\)).

Für \(\log_{e}p\) schreibt man kurz: \(\ln p\).

Allgemein gilt:

\(e^{a}=p\Leftrightarrow a=\ln p\) mit \(p\in\mathbb{R}^{+}\)

Der Logarithmus mit Basis \(e\) heißt natürlicher Logarithmus und wir notieren ihn mit \(\ln\).

Jede positive reelle Zahl \(q>0\) können wir als Exponential- oder Logarithmusterm angeben.

\(q=e^{\ln q}=\log_{e}e^{q}=\ln e^{q}\)

Damit können wir nun jeden Exponentialterm mit Basis \(q\in \mathbb{R}^{+}\) auf einen Exponentialterm mit Basis \(e\) zurückführen. Deshalb gelten die obigen Rechenregeln auch für jede beliebige Basis \(q\in \mathbb{R}^{+}\).

Allgemein gilt:

\(q=e^{\ln(q)}\), oder

\(q^{a}=\left(e^{\ln(q)}\right)^a=e^{\ln(q) \cdot a}\) mit \(q\in \mathbb{R}^{+}\)

Die erste Ableitung der natürlichen Exponentialfunktion bilden wir mit der Kettenregel.

\(f^{\prime}(x)={\underset{n\rightarrow\infty}{\lim}\left[n\left(1+\frac{x}{n}\right)^{n-1}\cdot\frac{1}{n}\right]}\)

\(\qquad=\underset{n\rightarrow\infty}{\lim}\left(1+\frac{x}{n}\right)^{n-1}=e^{x}=f(x)\) ; \(x\in\mathbb{R}\)

Allgemein gilt:

Die natürliche Exponentialfunktion ist in \(\mathbb{R}\) differenzierbar und es gilt:

\(f^{\prime}(x)=e^{x}\), sowie

\(\int e^{x}dx=e^{x}+C\) mit \(C\in\mathbb{R}\)

Weitere Ableitungen der natürlichen Exponentialfunktion ändern sich nicht.

\(f(x)=f^{\prime}(x)=f^{\prime\prime}(x)=f^{\prime\prime\prime}(x)=e^{x}>0\) für alle \(x \in\mathbb{R}\)

---

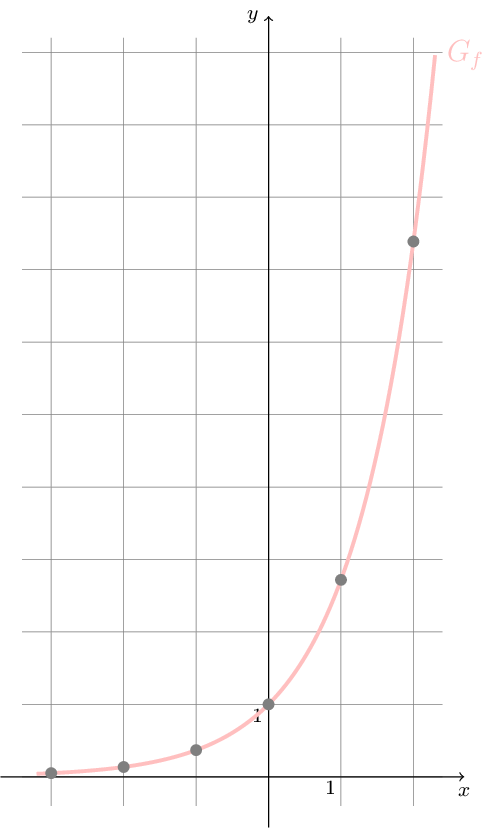
Wir rechnen \(e^{0}=1\) und somit schneidet der Graph der natürlichen Exponentialfunktion die \(y\)-Achse im Punkt \(A(0;1)\) und verläuft in \(\mathbb{R}\) oberhalb der \(x\)-Achse.

Da zusätzlich gilt: \(f^{\prime}(x)=f^{\prime\prime}(x)=e^{x}>0\), ist die natürliche Exponentialfunktion in \(\mathbb{R}\) echt monoton zunehmend und der Graph \(G_{f}\) der natürlichen Exponentialfunktion ist in \(\mathbb{R}\) linksgekrümmt. Außerden gibt es hier keine Extrem- und keine Wendepunkte.

---

Das Verhalten von \(f(x)\) an den Grenzen des Definitionsbereichs ist unterschiedlich.

\(\underset{x\rightarrow+\infty}{\lim}e^{x}=+\infty\)

\(\underset{x\rightarrow-\infty}{\lim}e^{x}=\underset{x\rightarrow-\infty}{\lim}\frac{1}{e^{-x}}=0\)

Die \(x\)-Achse ist horizontale Asymptote von \(G_{f}\).

Der Graph der natürlichen Exponentialfunktion ist streng monoton steigend und wir merken uns einige Funktionswerte, nämlich \(e^{-1}\approx 0.37\), \(e^{0}\approx 1\), \(e^{1}\approx 2.72\) und \(e^{2}\approx 7.39\).

Bei Berechnungen zur natürlichen Exponentialfunktion verwenden wir noch weitere Integrationsregeln.

• \(\int e^{f(x)}\cdot f^{\prime}(x)dx=e^{f(x)}+C\)

• \(\int e^{ax+b}dx=\frac{1}{a}\int e^{ax+b}\cdot a dx=\frac{1}{a}e^{ax+b}+C\)

Partielle Integration

• \(\int u(x)v^{\prime}(x)dx=u(x)v(x)-\int v(x)u^{\prime}(x)dx\)

• \(\int (ax+b)e^{mx+t}dx=\frac{1}{m}(ax+b)e^{mx+t}-\frac{a}{m}\int e^{mx+t}dx\)